Let
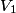 be the voltage at a point between the two leftmost resistors in the figure. There are only two resistors that are on horizontal line segments. Let be the voltage at a point between the two leftmost resistors in the figure. There are only two resistors that are on horizontal line segments. Let 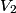 the voltage at a point between them. Let the voltage at a point between them. Let 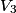 be the voltage at a point between two rightmost resistors in the figure. Then, using Kirchoff's junction rule, we have the following equations be the voltage at a point between two rightmost resistors in the figure. Then, using Kirchoff's junction rule, we have the following equations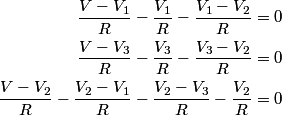 When we multiply both sides of these equations by 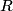 and then simplify, we obtain and then simplify, we obtain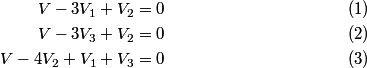 The first two equations, when subtracted, imply that 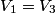 . Plugging this into equation (3) gives . Plugging this into equation (3) gives We can plug in 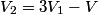 (from equation (1)) to solve for (from equation (1)) to solve for 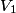 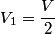 and then plug this back into equation (4) to get 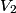 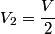 So, 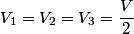 and the current through the battery is 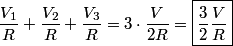 Therefore, answer (D) is correct. |